Mathematician Marcus du Sautoy was in search of the best language(s) to learn in order to pursue a career in espionage; it led him to the one language to unlock the greatest mysteries any spy could imagine: the mysteries of nature. He shares his thoughts on the language of mathematics…
When I was young I hadn’t wanted to be a mathematician at all. My dream when I grew up was to become a spy. This was partly the result of watching too many James Bond movies. But the inspiration also came from my mother. She’d been in the Diplomatic Service before she had started a family. I didn’t really understand what that meant but as I tried to piece together what my Mum had been doing before I was born, her stories all contributed to my belief that she too had been a spy.
To realise my dream of joining the world of international espionage I decided that I needed to try to learn as many languages as I could so that I could talk to my fellow spies across the world. So, when I went up to school, I started signing up for all the languages I could find. My school taught French, German, Latin (not too many Roman spies around these days but I’d been told that it was the root of many of the languages I was aspiring to learn). The BBC had just started a Russian course on TV which was great. I’m old enough to have grown up during the cold war, so, Russian seemed ideal for my spying aspirations. I got my French teacher to help me with the Russian course.
But, as time went on, I got more and more frustrated by these languages. There were so many words whose spellings were impossible to guess. Irregular verbs whose forms didn’t seem to have any logic to them.The whole thing seemed so inefficient. Multiple words all meaning the same things. Dog. Le chien. Der Hund. Canis. Собака. The Russian course I took was a disaster. I couldn’t get past the word for hello – здороваться – which, to my ear, sounded like an unpronounceable cacophony of consonants. Given that it was even the name of the course, I became seriously disillusioned with my dream of becoming a spy. I was on the look out for something that had an internal logic to it, something without irregular verbs.
It was my mathematics teacher who came to the rescue. In the middle of a lesson he suddenly pointed at me: “du Sautoy. I want to see you after the class.” I thought I was in trouble. When the lesson ended he took me around the back of the maths block, at which point I became seriously worried. But then he explained that this was where he smoked his breaktime cigar. He said to me, “du Sautoy, I think you should find out what mathematics is really about.”
He then went on to explain that it wasn’t really about the long division, the percentages, the sines and cosines we were doing in the classroom. He recommended a few books that he thought might unveil what mathematics was truly about. That weekend my father took me to the nearest academic bookshop located in Oxford to find the books my teacher had recommended. As my father worked his way through the list, I wandered around the mathematics shelves. I was very intrigued to see undergraduates leaning up against the shelves reading the mathematics books as if they were novels, engrossed in the stories they told. But when I picked books off the shelves, flicking through the pages to find out what was so fascinating, all I found were strange strings of symbols. It all seemed to be in code.
When I got home there was one book in particular that struck me immediately as intriguing. It was called The Language of Mathematics. I’d never before thought of mathematics as a language but as I read the book I began to understand what an extraordinary language mathematics is. It is the language of Nature. It is a language that can unlock the secrets of where we have come from, revealing the hidden stories of our past. But perhaps more excitingly it is a language that can help to predict the future. The equations of motion, when combined with the calculus, give scientists the potential to unlock the destiny of the universe. Best of all, this language made perfect logical sense. There were no irregular verbs. That’s not to say it was entirely predictable. It was a language full of surprises and unexpected twists and turns and yet everything made perfect logical sense. I had found the language that I would learn.
Galileo Galilei famously summed up the power of this language: “The universe cannot be read until we have learnt the language and become familiar with the characters in which it is written. It is written in mathematical language, and the letters are triangles, circles and other geometrical figures, without which means it is humanly impossible to comprehend a single word.”
One of the exciting discoveries for me was the revelation that this language is not simply a tool for describing what exists already but has the potential to create new structures that have never been imagined or seen before. I can still remember the thrill of using this language for the first time to “see” shapes in 4 dimensions. It is the great French philosopher Descartes who is responsible for creating the mathematical dictionary that made it possible for us to transcend our 3-dimensional universe. He developed the dictionary because of his frustration with how difficult it is to pin down the visual world. As he used to say: “Sense perceptions are sense deceptions”.
To deal with the problem of perception, Descartes created a powerful dictionary that translates geometry into numbers. When we look up the location of a town in an atlas we find it identified by a two number grid location. A GPS can pinpoint very accurately every location on the earth using a pair of numbers. These numbers pinpoint our North- South, East-West location from a point on the equator that lies directly south of Greenwich in London.
For example Kindle headquarters in Kolkata is on a latitude of 22.58 degrees north and 88.43degrees east. In Descartes’ dictionary we can translate the geographical location of Kindle HQ into two numbers or coordinates (22.58, 88.43).
We can use a similar process to describe mathematical shapes. For example, if I want to describe a square in terms of Descartes’ dictionary of coordinates I can say that it is shape with 4 vertices located at the points (0,0), (1,0), (0,1) and (1,1). The flat two dimensional world needs just two coordinates to locate each position, but if we also want to include our height above sea-level then we could add a third coordinate. We will need this third coordinate too if we want to describe a three-dimensional cube in terms of coordinates. It’s eight vertices can be described by the coordinates (0,0,0), (1,0,0), (0,1,0), (0,0,1), (1,1,0), (1,0,1), (0,1,1) and finally the extremal point at (1,1,1).
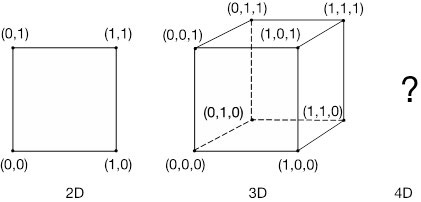
Descartes’ dictionary has shapes and geometry on one side and, on the other, it has numbers and coordinates. The trouble is that the visual side runs out if we try to go beyond 3-dimensional shapes, since there isn’t a fourth physical dimension where I can see higher dimensional shapes. It was the great nineteenth century German mathematician Bernhard Riemann who recognized that the beauty of Descartes’ dictionary is that the other side of the dictionary keeps going.
To describe a four dimensional object I just add a fourth coordinate which would just keep track of how far you are moving in this new direction. So, although I can never physically build a 4-dimensional cube, by using numbers I can still describe it precisely. It has 16 vertices starting at (0,0,0,0) then extending to points at (1,0,0,0), (0,1,0,0) and stretching out to the furthest point at (1,1,1,1). The numbers are a code to describe the shape. And using this code I can explore the shape without ever having to physically see it.
And it doesn’t stop there. You can move into 5, 6 or even higher dimensions and build hypercubes in these worlds. For example a hypercube in N dimensions will have 2^N vertices. Out of each of these vertices there will be N edges emerging, each of which I am counting twice. So the N-dimensional cube has N x 2^(N-1) edges. We can find ways to get glimpses of these surreal shapes in our mundane three dimensional world. La Grande Arche at la Defence in Paris, built by the Danish architect Johann Otto von Spreckelsen, is actually a shadow of a four dimensional cube, a cube inside a cube. Salvador Dalí, in his painting Crucifixion (Corpus Hypercubus), depicts Christ crucified on the three-dimensional net of a fourdimensional cube.
But it is only with mathematical language that we can truly navigate the contours of these shapes that transcend our physical space. Although ultimately I may have failed in my dream to become a spy, I believe that the language I have dedicated my life to speaking has unlocked the secrets of a far more fascinating and universal world.
Marcus du Sautoy is Professor of Mathematics at the University of Oxford and author of The Music of the Primes, Finding Moonshine and The Number Mysteries.


